Greedy Algorithmen

Wir widmen uns den in gewisser Hinsicht einfachst möglichen Algorithmen: Greedy Algorithmen. Diese versuchen ein Problem völlig naiv wie folgt zu lösen: Die Lösung wird einfach nach und nach zusammengesetzt und dabei wird in jedem Schritt der momentan beste Folgeschritt ausgewählt. Es wird nicht darauf geachtet, was langfristig gut ist, sondern der Algorithmus ist in dem Sinne gierig (daher der Name), dass er einfach das lokal Nächstbeste tut. Erstaunlicherweise funktioniert dieser Ansatz auf einigen Problemen, denen man dies so nicht ansieht, d.h. die eigentlich deutlich schwieriger aussehen. Ein großer Vorteil von Greedy Algorithmen gegenüber anderen Ansätzen ist, dass Greedy Algorithmen meist sehr schnell und gleichzeitig leicht zu implementieren sind.

Greedy Algorithmen zu entwerfen, ist leicht. Für so gut wie jedes Problem ist ein solcher Ansatz meist die erste Idee, die uns einfällt. Viel schwieriger ist es allerdings, zu erkennen, wann ein solch naiver Ansatz wie ein Greedy Algorithmus tatsächlich funktioniert, um die bestmögliche Lösung zu finden. Generell gilt folgende Grundregel:

Jeder Greedy Algorithmus ist mit äußerster Vorsicht zu betrachten. Vertraue einem Greedy Algorithmus nur, wenn du seine Korrektheit bewiesen hast!

Um uns heranzutasten, werden wir nun zwei Probleme aus dem Bereich des Scheduling betrachten und für diese Greedy Algorithmen entwickeln und analysieren. Beim Scheduling geht es darum, dass man Ressourcen (z.B. Hörsäle, Drucker oder Maschinen) und Jobs (z.B. Vorlesungen, Druck- oder Fertigungsaufträge) hat und die Jobs möglichst gut mit den vorhandenen Ressourcen abarbeiten will.

Problem 1: Planung von Vorlesungen

Wir betrachten das folgende sehr einfache Problem:

Geg.: Die Start- und Endzeiten von \(n\) Vorlesungen als Paare \((s(i),e(i))\) für \(1 \leq i \leq n\).

Aufgabe: Verteile die Vorlesungen so auf eine Menge von Hörsälen, so dass möglichst wenige Hörsäle benutzt werden und sich keine Vorlesungen im selben Hörsaal überschneiden.

Wir können uns das Problem auch leicht visualisieren:

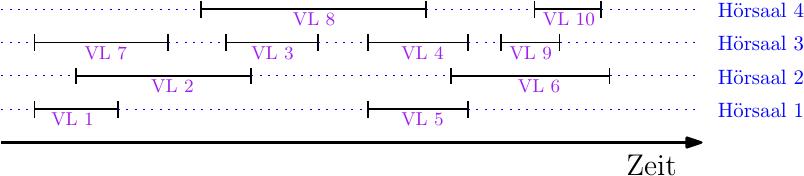
Hierbei haben wir ein Zeitintervall für jede Vorlesung und die Intervalle überlappen sich, wenn sich die Vorlesungszeiten überlappen. Im obigen Beispiel sehen wir eine Zuweisung der Vorlesungen zu Hörsälen, die zulässig ist, d.h. keine Vorlesungen im selben Hörsaal überschneiden sich, und die insgesamt 4 Hörsäle benötigt.

Es ist leicht zu sehen, dass es für unser Problem eine bessere Lösung gibt:

Wir können alle 10 Vorlesungen auch auf nur 3 Hörsäle zulässig zuweisen!

Sofort stellt sich die Frage, ob es nicht noch besser geht. Bei der obigen Instanz ist das unmöglich, denn es gibt drei Vorlesungen (z.B. VL 1, VL 2 und VL 7) die sich alle zeitlich überlappen. D.h. für diese drei Vorlesungen benötigen wir auf jeden Fall drei verschiedene Hörsäle. Wir haben somit ein Maß gefunden, welches uns etwas darüber sagt, wieviele Hörsäle wir mindestens benötigen:

Die Tiefe einer Instanz sei die maximale Zahl der Vorlesungen, die sich zu irgendeinem Zeitpunkt überlappen. In unserem Beispiel ist die Tiefe 3 und es gibt mehrere Zeitpunkte, an denen die Überlappung maximal ist:

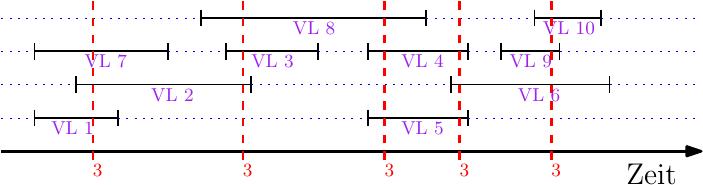
Es gilt:

Lemma 1. Jede Instanz mit Tiefe \(d\) benötigt mindestens \(d\) Hörsäle.

Wir haben somit eine untere Schranke an die Anzahl der benötigten Hörsäle. Doch es ist nicht unbedingt offensichtlich, dass jede Instanz mit Tiefe \(d\) auch tatsächlich eine zulässige Lösung mit \(d\) Hörsälen besitzt. Die Intervalle könnten sich ja irgendwie seltsam gegenseitig beeinflussen.

Wir zeigen nun, dass es tatsächlich immer mit \(d\) Hörsälen geht. Die Lösung ist ein ganz einfacher Greedy Algorithmus. Die Idee ist hierbei, dass wir die Vorlesungen nach aufsteigender Zeit durchlaufen und immer den freien Hörsaal mit der kleinsten Nummer an die jeweilige Vorlesung vergeben.

  \begin{algorithmic}
     \STATE{initialisiere Array \(H\) der Länge \(n\)}
     \STATE{berechne die Tiefe \(d\)}
     \STATE{\(V' \leftarrow\) sortiere \(V\) aufsteigend nach Startzeit (löse Gleichstände beliebig auf)}
     \FOR{Vorlesung \(j=1\) to \(n\) aus \(V'\)}
    \STATE{\(Nr(j) \leftarrow\) Nummer der \(j\)-ten Vorlesung aus \(V'\)}
    \STATE{\(H[Nr(j)] \leftarrow\) kleinste Hörsaalnummer aus \(\{1,...,d\}\) die an keine der Vorlesungen aus \(V'\) vergeben wurde, die Vorlesung \(j\) überlappen und früher beginnen}
     \ENDFOR
     \RETURN{\(H\)}
  \end{algorithmic}
  

Falls der obige Algorithmus terminiert, dann erzeugt er eine zulässige und optimale Lösung. Die Lösung ist zulässig, da an sich überlappende Vorlesungen garantiert unterschiedliche Hörsäle vergeben werden. Die Lösung ist optimal, da nur \(d\) Hörsäle benötigt werden. In unserem Beispiel würden wir folgende Lösung erhalten:

Wir müssen somit nur noch beweisen, dass der obige Algorithmus terminiert, d.h. dass in der for-Schleife immer eine Hörsaalnummer übrig ist.

Lemma 2. Der Algorithmus Greedy-Hörsaalvergabe terminiert immer.

Beweis. Wir beweisen die Aussage per Widerspruch:
Angenommen für die \(j\)-te Vorlesung aus \(V'\) kann keine Hörsaalnummer vergeben werden. Das bedeutet, dass es mindestens \(d\) viele Vorlesungen gibt, die sich alle mit Vorlesung \(j\) überschneiden und die zum Zeitpunkt als Vorlesung \(j\) an die Reihe kommt, bereits eine Hörsaalnummer erhalten haben (und diese somit blockieren). Es gibt somit mindestens \(d\) Vorlesungen, die früher begonnen haben und sich mit Vorlesung \(j\) überschneiden. Folglich gibt es einen Zeitpunkt (nämlich den Startzeitpunkt von Vorlesung \(j\)) an dem sich \(d+1\) viele Vorlesungen überlappen. Dies ist ein Widerspruch zu unserer Wahl von \(d\).

Wir hatten bei diesem Problem recht leichtes Spiel. Durch die Tiefe einer Instanz hatten wir eine untere Schranke an die Anzahl der Hörsäle. Für die Optimalität unseres Algorithmus mussten wir nur noch zeigen, dass wir diese untere Schranke genau treffen können.

Problem 2: Druckjobs planen

Wir betrachten nun ein Problem, bei dem wir keine Hilfestellung in Form einer speziellen Eigenschaft der Instanzen bekommen.

Wir betrachten eine Großdruckerei, die einen Spezialdrucker so auslasten möchte, um damit möglichst viele Jobs abzuarbeiten. Jeder Job hat eine Startzeit und eine Druckdauer - somit können wir einfach wieder von Start- und Endzeiten ausgehen.

Geg: \(n\) Druckjobs mit Start- und Endzeiten \((s(i),e(i))\), für \(1\leq i \leq n\).

Aufgabe: Finde die größtmögliche Menge von sich paarweise nicht überlappenden Jobs.

Wir treffen hier also die Annahme, dass unser Drucker pro Zeitpunkt immer nur einen Job abarbeiten kann. Falls sich mehrere Jobs zu einem Zeitpunkt überlappen, dann müssen alle bis auf einen abgelehnt werden (es gibt somit keine Warteschlange).

Auf dem Weg zu einem Greedy Algorithmus können wir einfach ein paar einfache aber plausible Ideen durchtesten:

• Wir können einfach mit dem frühesten Job beginnen, alle überlappenden Jobs verwerfen und mit dem nächst frühesten Job weitermachen. Leider funktioniert das nicht:

  

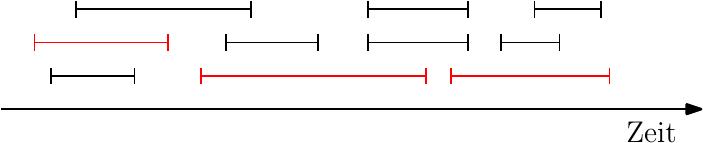
  Der Algorithmus würde hier nur 3 anstatt 4 Jobs auswählen. Es kommt sogar noch schlimmer, der Algorithmus könnte beliebig schlecht werden, d.h. 1 anstatt \(n-1\) viele Jobs auswählen:

  

• Das Problem im obigen Ansatz sind Jobs, die sehr lange dauern. Wie wäre es also, wenn wir mit dem kürzesten Job beginnen, alle überlappenden verwerfen und den nächst kürzesten nehmen, usw.? Leider funktioniert das auch nicht:

  

  Der Algorithmus würde nur 4 statt 8 Jobs auswählen.

• Das Problem des obigen Ansatzes ist, dass sich ein kurzer Job mit mehreren anderen Jobs überlappen kann und wir im Beispiel gerade die Jobs ausgewählt haben, die die meisten Überlappungen haben. Dies bringt uns zur nächsten Idee: Wir berechnen für jeden Job die Anzahl der anderen Jobs, mit denen es eine Überlappung gibt. Dann beginnen wir mit dem Job mit den wenigsten Überlappungen, verwerfen alle überlappenden Jobs und fahren iterativ so fort. Leider funktioniert auch das nicht:

  

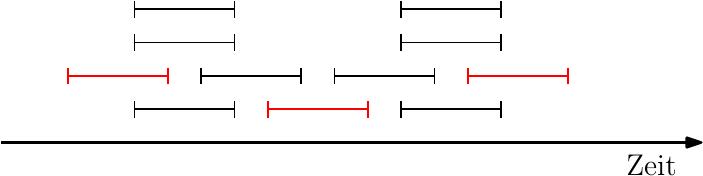
  Hier würde der Algorithmus 3 statt 4 Jobs auswählen. Das Problem ist hier, dass der mittlere Job die wenigsten Überlappungen hat.

Wir sehen somit, dass es viele plausible Ideen gibt, die allerdings alle nicht zu einem bestmöglichen Algorithmus führen. Tatsächlich gibt es eine weitere plausible Idee, die funktioniert:

Wähle immer den Job, der den frühesten Endzeitpunkt hat, entferne alle überlappenden Jobs und fahre iterativ fort, bis keine Jobs mehr verfügbar sind.

Die Idee ist also, die Ressource immer so schnell wie möglich wieder freizugeben, um somit Platz für möglichst viele spätere Jobs zu schaffen. Das klingt vernünftig, doch wir hatten auch für alle anderen Ideen von oben eine vernünftige Begründung.

Zuerst sehen wir, dass dieser Greedy-Algorithmus in all den obigen Beispielen die korrekte Lösung liefert. Wir müssen allerdings ausschließen, dass wir auch diesmal wieder ein Gegenbeispiel konstruieren können! Wir benötigen einen Korrektheitsbeweis. Für diesen benutzen wir eine interessante Beweisstrategie, die man greedy stays ahead nennt.

Korrektheitsbeweis mit greedy stays ahead

Um zu zeigen, dass unser Greedy-Algorithmus die bestmögliche Lösung liefert, müssen wir nur beweisen, dass wir genausoviele Jobs drucken können, wie der optimale Algorithmus (der z.B. per Brute-Force arbeitet). Es kann mehrere bestmögliche Lösungen geben, wichtig ist allerdings nur, wieviele Jobs gedruckt werden können.

Sei \(J^*\) die Menge der Jobs, die der optimale Algorithmus druckt und sei \(J\) die Menge der Jobs, die unser Greedy-Algorithmus auswählt. Wir müssen also \(|J| = |J^*|\) zeigen.

Unser Greedy-Algorithmus arbeitet die Jobs nach aufsteigendem Endzeitpunkt ab, d.h. er wählt anfangs einen Job aus, dann einen Job, der später startet, usw. Unser Greedy-Algorithmus erweitert also immer eine bestehende partielle Lösung um einen weiteren später endenden Job (Da wir keine Überlappungen haben, muss dieser Job auch erst nach Beendigung des spätesten Jobs in der partiellen Lösung starten). Die partielle Lösung ist somit die Lösung des Greedy-Algorithmus für eine Teilmenge der Jobs, nämlich genau für diejenigen Jobs, deren Endzeitpunkte alle vor einem Zeitpunkt \(t\) liegen.

Wir betrachten, was im obigen Beispiel passiert:

Nun kommt das greedy stays ahead Argument: Für jeden Zeitpunkt \(t\) können wir die aktuelle partielle Lösung des Greedy Algorithmus mit der partiellen optimalen Lösung \(J^*\), die nur Jobs aus \(J^*\) enthält, die bis zum Zeitpunkt \(t\) beendet sind, vergleichen. Falls für jeden Zeitpunkt \(t\) die aktuelle partielle Lösung unseres Greedy Algorithmus mindestens so gut ist wie die partielle Lösung des optimalen Algorithmus, dann gilt für \(t=\infty\) (Hier genügt ein \(t\), welches größer ist als der Endzeitpunkt des am spätesten endenden Jobs), dass \(|J| \geq |J^*|\). Da \(J^*\) eine optimale Lösung ist, folgt \(|J| = |J^*|\).

Für unseren Beweis nehmen wir an, dass \(i_1,\dots,i_k\) die Jobs aus \(J\) sind, wobei \(i_1\) der erste zur Lösung hinzugefügte Job ist, \(i_2\) der zweite, usw. Somit gilt \(|J| = k\). Analog dazu nehmen wir an, dass \(j_1,\dots,j_m\) die Reihenfolge der Jobs aus \(J^*\) ist, wobei \(j_1\) der früheste Job aus \(J^*\) ist und \(j_m\) der späteste. Da \(J^*\) eine zulässige Lösung ist, muss somit \(j_1\) einen früheren Start- und Endzeitpunkt als \(j_2\) haben, usw.

Unser Greedy Algorithmus wählt den ersten Job so, dass der Drucker so schnell wie möglich wieder frei wird. Folglich gilt \(e(i_1) \leq e(j_1)\). In diesem Sinne soll der Greedy Algorithmus also immer vor dem optimalen Algorithmus bleiben. Allgemein soll folgendes gelten:

Lemma 3. Für alle \(r \leq k\) gilt: \(e(i_r) \leq e(j_r)\).

Beweis. Die Form der Aussage legt einen Beweis per Induktion über \(r\) nahe. Für \(r=1\) gilt die Aussage, da unser Greedy Algorithmus per Definition den Job mit dem frühesten Endzeitpunkt wählt. Betrachten wir nun den Induktionsschritt von \(r-1\) nach \(r\) für ein beliebiges \(2 \leq r\leq k\): Wir nehmen nach Induktionsvoraussetzung an, dass \(e(i_{r-1}) \leq e(j_{r-1})\) gilt. Wir wollen nun zeigen, dass daraus folgt, dass \(e(i_r) \leq e(j_r)\) gilt. Wir zeigen dies per Widerspruch. Dafür überlegen wir uns, was passieren müsste, damit die Behauptung nicht stimmt. Wir hätten in dem Fall folgende Situation:

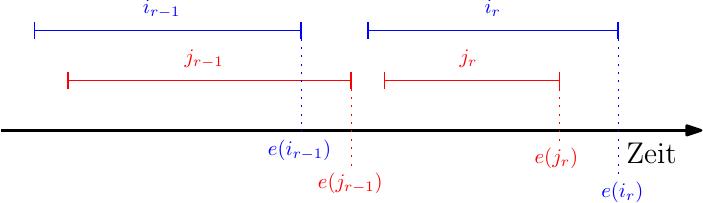
Wir sehen schon an der Abbildung, dass diese Situation nicht eintreten kann, denn der Greedy Algorithmus hätte in dieser Situation nicht \(i_r\) sondern \(j_r\) gewählt, da dieser früher endet und später als \(e(i_{r-1})\) beginnt. Letzteres gilt, da nach IV \(e(i_{r-1}) \leq e(j_{r-1})\) gilt, und da sich in \(O\) keine Jobs überlappen muss \(e(j_{r-1}) \leq s(j_{r})\) gelten. Somit haben wir \(e(i_{r-1}) \leq e(j_{r-1}) \leq s(j_{r})\) und folglich einen Widerspruch.

Nun beweisen wir, dass unser Greedy Algorithmus eine optimale Lösung erzeugt:

Theorem 1. Es gilt \(|J| = |J^*|.\)

Beweis. Wir beweisen die Aussage per Widerspruch. Angenommen \(J\) ist keine optimale Lösung, d.h. es gilt \(|J| \lt |J^*|\) und somit muss \(k \lt m\) gelten. Wenn wir nun Lemma 3 mit \(r = k\) anwenden, dann erhalten wir, dass \(e(i_k) \leq e(j_k)\) gilt. Da \(m \gt k\), muss es also einen Job \(j_{k+1}\) in \(J^*\) geben, der nach \(e(j_k)\) beginnt. Da \(e(i_k) \leq e(j_k)\), beginnt \(j_{k+1}\) somit auch nach \(e(i_k)\). D.h. nachdem der Greedy Algorithmus alle mit Job \(i_k\) überlappenden Jobs entfernt hat, muss Job \(j_{k+1}\) noch übrig sein. Der Greedy Algorithmus hätte somit nicht bei Job \(i_k\) gestoppt, da es noch verfügbare (zulässige) Jobs gibt. Wir haben somit einen Widerspruch.

Implementierung des Greedy Algorithmus

Nachdem wir nun überzeugt sind, dass unser Greedy Algorithmus die optimale Lösung erzeugt, müssen wir diesen nur noch geeignet implementieren. Dies ist einfach:

  \begin{algorithmic}
     \STATE{Sortiere die Jobs aufsteigend nach Endzeitpunkt. Sei \(x_1,...,x_n\) diese Reihenfolge.}
     \STATE{\(J \leftarrow \{x_1\} \)}
     \STATE{\(e \leftarrow e(x_1)\)}
     \FOR{\(i=2\) to \(n\)}
       \IF{\(s(x_i) \geq e\)}
         \STATE{\(J \leftarrow J \cup \{x_i\} \)}
         \STATE{\(e = e(x_i)\)}
       \ENDIF
     \ENDFOR
     \RETURN{\(J\)}
  \end{algorithmic}
  

Das Sortieren kostet uns \(O(n\log n)\), die Schleife \(O(n)\). Insgesamt haben wir Kosten in \(O(n\log n)\).