Binäre Heaps und Heapsort
Heapsort
Wir betrachten einen Sortieralgorithmus, der einerseits Worstcase-Kosten von \(O(n\log n)\) hat und gleichzeitig nur \(O(1)\) Speicherplatz benötigt. Die Idee von Heapsort ist es, eine geeignete Datenstruktur — einen Heap — zu benutzen und mithilfe dieser Datenstruktur zu sortieren. Der clevere Trick hierbei ist, dass die Datenstruktur direkt im gegebenen Array realisiert werden kann. Das heißt, wir benötigen dafür keinen zusätzlichen Speicherplatz.
Bevor wir zum Sortieralgorithmus kommen, müssen wir uns also zunächst näher mit Heaps beschäftigen.
Binäre Heaps
Es gibt viele Varianten von Heaps, doch wir werden uns zunächst nur mit der einfachsten Variante, den sogenannten binären Heaps beschäftigen. Davon gibt es zwei Varianten: Min-Heaps und Max-Heaps.
Ein Heap — Englisch für Haufen — ist ein spezieller gerichteter Binärbaum. Das heißt, wir treffen nun zum ersten Mal eine Datenstruktur an, die auf einem (gerichteten) Graphen basiert. Wir werden später sehen, dass wir für Heaps den Graphen eigentlich gar nicht benötigen. Allerdings hilft er uns, um genau zu verstehen, wie ein Heap funktioniert.
Ein gerichteter Graph ist eine Menge von Knoten und gerichteten Kanten, wobei Knoten spezielle Objekte sind, die die Daten (z. B. die zu sortierenden Elemente) enthalten, und Kanten Referenzen zwischen den Knoten sind. Das heißt, Kanten sind eigentlich nur Zeiger, die von einem Knotenobjekt auf ein anderes Knotenobjekt verweisen. Jedes Knotenobjekt hat eine eindeutige Adresse bzw. ID und wir gehen davon aus, dass pro Knotenobjekt der Wert von genau einem zu sortierenden Element, der sogenannte Schlüssel, gespeichert ist. Jedes Knotenobjekt hat neben den Daten noch spezielle Zeiger, nämlich einen Zeiger auf den Vaterknoten, auf das linke Kind und auf das rechte Kind.

Wir gehen davon aus, dass es genau einen Knoten gibt, der keinen Vater hat (d. h., der Vater-Zeiger zeigt auf null). Diesen Knoten nennen wir Wurzel und wir bezeichnen Knoten, die keine Kinder haben, als Blätter. Ein gerichteter Binärbaum ist eine Menge von Knotenobjekten und Zeigern, so dass es genau eine Wurzel gibt und alle Knotenobjekte so miteinander verbunden sind, dass keine Kreise entstehen. Das heißt, für zwei benachbarte Knoten ist immer klar, wer der Vater und wer der Sohn ist. Wir zeichnen gerichtete Binärbäume immer so, dass ein Vaterknoten jeweils über seinen Kindern steht und das linke Kind links vom Vater und das rechte Kind rechts vom Vater liegt. null-Zeiger lassen wir in den Darstellungen einfach weg und wir zeichnen nur die Zeiger vom Vater zu seinen Kindern. Folglich ist die Wurzel eines gerichteten Binärbaums immer ganz oben.

Ein besonderer gerichteter Binärbaum ist der vollständige Binärbaum. Bei ihm haben alle Knoten, außer die Knoten im letzten Level, genau zwei Kinder und die Knoten im letzten Level haben gar keine Kinder.
Die Struktur eines Min- bzw. Max-Heaps ist der eines vollständigen Binärbaums sehr ähnlich: Ein Min/Max-Heap hat die Struktur eines Binärbaums, der bis zum vorletzten Level vollständig ist und das letzte Level von links her gefüllt sein muss. (Wir werden später sehen, warum wir diese Eigenschaft unbedingt benötigen.) Außerdem muss in einem Min-Heap die Min-Heap-Eigenschaft gelten und in einem Max-Heap die Max-Heap-Eigenschaft. Die Min-Heap-Eigenschaft besagt, dass der Schlüsselwert eines Vaterknotens immer höchstens so groß ist, wie der Schlüsselwert jedes seiner Kinder. Analog gilt für die Max-Heap-Eigenschaft, dass der Schlüsselwert eines jeden Vaterknotens immer mindestens so groß sein muss, wie der Schlüsselwert jedes seiner Kinder.
Aus diesen Eigenschaften folgt direkt, dass die Wurzel eines Min-Heaps den kleinsten Schlüsselwert, d. h. das Minimum über alle Schlüssel, enthalten muss. Bei einem Max-Heap enthält die Wurzel das Maximum über alle Schlüssel.
Man beachte auch, dass für die Schlüsselwerte der Kinder eines Knotens in einem Min/Max-Heap nur gilt, dass ihre Schlüsselwerte mindestens/höchstens so groß sind, wie die ihres Vaters — jedoch wird nicht gefordert, dass das linke Kind den kleinsten/größten Schlüsselwert aller Kinder hat oder ähnliches. Die Min/Max-Heap-Eigenschaft sagt nur etwas darüber aus, wie sich die Schlüsselwerte von direkt benachbarten Knoten verhalten, über die Schlüsselwerte innerhalb eines Levels wird nichts ausgesagt. (Solche Aussagen werden wir später noch bei Suchbäumen antreffen.)
Um mit Min/Max-Heaps zu arbeiten, müssen wir uns überlegen, wie wir aus einer Folge von Schlüsselwerten einen korrekten Min/Max-Heap erzeugen können. Das wird die Operation BuildMinHeap bzw. BuildMaxHeap erledigen. Außerdem wollen wir in einem Min-Heap das Minimum entfernen, d. h., die Operation ExtractMin umsetzen, und in einem Max-Heap das Maximum entfernen, d. h., die Operation ExtractMax implementieren. (Später werden wir Min-Heaps benutzen, um damit spezielle Queues zu konstruieren und dazu noch die Operationen Insert und DecreaseKey hinzufügen.)
BuildHeap
Wir wollen das folgende Problem lösen:
\begin{quote}
Gegeben: Ein Array \(A\) mit \(n\) Schlüsselwerten.
Aufgabe: Konstruiere aus \(A\) einen korrekten Min/Max-Heap, der alle Schlüsselwerte von \(A\) enthält.
\end{quote}
Das Problem kann man mit den folgenden zwei Schritten sehr elegant lösen:
- Erzeuge einen Binärbaum mit der richtigen Form, wobei die Knoten die Schlüssel aus dem Array \(A\) enthalten.
- Teste für jeden Knoten, ob die Min/Max-Heap-Eigenschaft gilt. Falls sie nicht gilt, dann stelle sie her.
BuildMinHeap(\(A\))
Input: Array \(A\) der Länge \(n\)Output:Min-Heap mit allen Elementen aus \(A\)
\begin{algorithmic}
\STATE{erzeuge Binärbaum \(T\) der richtigen Form, der in jedem Knoten genau einen Schlüsselwert von \(A\) enthält}
\FOR{Level=vorletztes Level to erstes Level}
\FOR{Knoten=rechtester Vater in Level to linkester Vater in Level}
\STATE{\textsf{MinVersickere}(Knoten)}
\ENDFOR
\ENDFOR
\RETURN \(T\)
\end{algorithmic}
Hierbei ist bei Zeile \(1\) eben genau ein bis zum vorletzten Level vollständiger gerichteter Binärbaum gemeint, bei dem das letzte Level von links her gefüllt ist. Wichtig ist, dass wir mit MinVersickere beim rechtesten Vaterknoten im vorletzten Level beginnen, d. h. beim rechtesten Knoten im vorletzten Level von \(T\), der mindestens ein Kind hat.
Nun klären wir noch, was genau MinVersickere tut. Wir betrachten den Code und ein Beispiel parallel:
MinVersickere(Knoten~$i$)
Input: Zeiger auf Knoten $i$
\begin{algorithmic}
\STATE{$key \leftarrow$ Schlüsselwert von Knoten~$i$}
\IF{Knoten $i$ ist Vater}
\STATE{$j \leftarrow$ Kind von $i$ mit kleinstem Schlüsselwert}
\IF{Knoten $j$ hat kleineren Schlüsselwert als $i$}
\STATE{vertausche Schlüsselwerte von Knoten $j$ und Knoten $i$}
\STATE{\textsf{MinVersickere}(Knoten $j$)}
\ENDIF
\ENDIF
\end{algorithmic}

Analog definieren wir BuildMaxHeap, wobei dort statt MinVersickere die Subroutine MaxVersickere genutzt wird:
MaxVersickere(Knoten~$i$)
Input: Zeiger auf Knoten $i$
\begin{algorithmic}
\STATE{$key \leftarrow$ Schlüsselwert von Knoten~$i$}
\IF{Knoten $i$ ist Vater}
\STATE{$j \leftarrow$ Kind von $i$ mit größtem Schlüsselwert}
\IF{Knoten $j$ hat größeren Schlüsselwert als $i$}
\STATE{vertausche Schlüsselwerte von Knoten $j$ und Knoten $i$}
\STATE{\textsf{MaxVersickere}(Knoten $j$)}
\ENDIF
\ENDIF
\end{algorithmic}

Entscheidend dafür, dass BuildHeap für beide Versionen korrekt funktioniert, ist, dass die Söhne eines Knotens immer schon vorher mit Min/MaxVersickere bearbeitet worden sind, bevor der Knoten selbst an die Reihe kommt. Das ist der Grund, warum wir im vorletzten Level mit dem Versickern beginnen und uns dann Level für Level nach oben durcharbeiten.
Betrachten wir ein vollständiges Beispiel für BuildMinHeap. Dazu nehmen wir an, dass das Array \(A = [68,18,29,12,25,15]\) ist. Zunächst erzeugen wir einen gerichteten Binärbaum, der die richtige Form hat und die Schlüssel von \(A\) enthält. Das heißt, er muss genau \(6\) Knoten enthalten und bis auf das letzte Level vollständig sein. Außerdem muss das letzte Level von links her gefüllt sein. Nach Zeile \(1\) von BuildMinHeap erhalten wir somit den folgenden Baum:

Nun beginnen wir im vorletzten Level mit dem rechtesten Vater und führen MinVersickere aus. Wir erhalten:

Danach kommt der nächste Vater im selben Level an die Reihe:

Danach wird die Wurzel versickert:

Danach sind wir fertig. Es wurde für alle Vaterknoten ab dem vorletzten Level einmal MinVersickere aufgerufen. Offensichtlich hängen die Kosten von BuildMinHeap somit sehr stark von den Kosten für MinVersickere ab. Die sind jedoch leicht zu ermitteln. Die Höhe eines Knotens \(i\) in einem gerichteten Binärbaum sei die Anzahl der Kanten auf dem längsten Pfad von Knoten \(i\) zu einem Blatt des Baums, wobei jeder Schritt des Pfads immer von einem Vater zu einem Kind dieses Vaters geht. Im obigen Min-Heap wäre die Höhe des Knotens mit Schlüssel \(12\) genau \(2\), da z. B. der Pfad \(12 \to 18 \to 25\) maximal lang ist und zu einem Blatt führt. Die Höhe eines Blattes ist immer \(0\).
Mithilfe der Höhe eines Knotens können wir leicht die Kosten von Min/MaxVersickere bestimmen: Die Kosten von Min/MaxVersickere(Knoten \(i\)) sind in \(\Theta(\)Höhe von Knoten \(i)\). Der Grund hierfür ist, dass für jede Kante auf dem Weg von Knoten \(i\) zum tiefsten Blatt, das unterhalb von \(i\) liegt, eine Vertauschung der Schlüsselwerte erfolgen kann. Außerdem kann jeweils der kleinste/größte Schlüsselwert der maximal zwei Kinder eines Vaterknotens in konstanter Zeit ermittelt werden.
Kommen wir nun zu den Kosten von BuildMinHeap — die Kosten von BuildMaxHeap lassen sich analog analysieren und sind identisch.
Wir wollen folgendes zeigen:
\begin{theorem}\label{thm_buildheap}
BuildMinHeap(\(A\)) hat Kosten in \(\Theta(n)\) für ein Array \(A\) der Länge \(n\).
\end{theorem}
Um den Beweis zu führen, benötigen wir noch eine Eigenschaft von vollständigen Binärbäumen:
Lemma 1. Ein vollständiger Binärbaum hat in Level \(i\) genau \(2^i\) viele Knoten, wobei Level \(0\) das Level der Wurzel ist.
\begin{proof}
Wir zeigen die Aussage per Induktion über \(i\):
IA: Für \(i=0\) gilt die Aussage, da das \(0\)-te Level genau einen Knoten, nämlich die Wurzel, enthält und \(2^0 = 1\).
IS (\(i \to i+1\)): Wir wollen zeigen, dass das \(i+1\)-te Level genau \(2^{i+1} = 2\cdot 2^i\) Knoten enthält. Nach Induktionsvoraussetzung wissen wir, dass das \(i\)-te Level, d. h. das Level oberhalb des \(i+1\)-ten Levels, genau \(2^i\) viele Knoten enthält. Da wir einen vollständigen Binärbaum betrachten, muss jeder Knoten in Level \(i\) genau zwei Kinder haben. Außerdem müssen alle Kinder von allen Vätern aus Level \(i\) paarweise unterschiedlich sein, da sonst ein Kreis entstehen würde (und die Eigenschaft, dass jedes Kind genau einen Vater hat, verletzt würde). Da jeder Knoten in Level \(i+1\) das Kind eines Vaters aus Level \(i\) ist, folgt, dass es genau \(2\cdot 2^i = 2^{i+1}\) viele Knoten in Level \(i+1\) gibt.
\end{proof}

Daraus folgt für einen vollständigen Binärbaum mit Höhe \(h\), dass \[n = \sum_{i = 0}^{h}2^i = 2^{h+1}-1\] gilt. Daraus folgt direkt, dass der längste Pfad von der Wurzel zu einem Blatt in einem Min-Heap mit \(n\) Knoten höchstens \(\lfloor \log n \rfloor\) viele Kanten besitzt. Das heißt, die Wurzel hat höchstens Höhe \(\lfloor \log n \rfloor\). Der Grund hierfür ist, dass laut Lemma 1 folgendes gilt: \[\sum_{i=0}^h 2^i = 2^{h+1}-1 \leq n \iff h+1 \leq \log (n-1) \iff h \leq \log(n-1)-1\ .\] Und \(h \leq \log(n-1)-1 \leq \log n -1 \leq \lfloor\log n\rfloor\).
Es gibt \(2^h\) viele Knoten mit Höhe \(0\) und offensichtlich gilt \(2^h \leq n = \frac{n}{2^{h-h}} = \frac{n}{2^0}\). Da es laut Lemma 1 genau halb so viele Knoten mit Höhe \(1\) gibt, wie es Knoten mit Höhe \(0\) gibt, folgt \(2^{h-1} \leq \frac{n}{2} = \frac{n}{2^{h-(h-1)}}\). Allgemein gilt, dass es höchstens \(\frac{n}{2^{h-i}}\) viele Knoten mit Höhe \(i\) gibt.
Nun können wir Theorem 1 beweisen:
\begin{proof}
Zunächst analysieren wir Zeile \(1\) von BuildMinHeap. Die können wir leicht mithilfe einer Queue mit Kosten \(\Theta(n)\) realisieren. Das Erzeugen eines Knotenobjekts kostet \(\Theta(1)\). Wir erzeugen erst die Wurzel und speichern darin den ersten Schlüssel aus \(A\). Außerdem erzeugen wir eine leere Queue. Die Wurzel (bzw. ein Zeiger auf das entsprechende Objekt bzw. die Objekt-ID) wird in die Queue eingefügt. Dann wiederholen wir folgendes so lange, bis wir genau \(n\) Knoten erzeugt und jedes Element aus \(A\) untergebracht haben: Wähle den Knoten \(x\), der in der Queue ganz vorn ist, erzeuge ein neues Knotenobjekt, füge das nächste Element aus \(A\) ein und setze den Linkes-Kind-Zeiger von \(x\) auf das neue Objekt. Füge das neue Objekt in die Queue ein. Falls noch nicht \(n\) Objekte erzeugt wurden, dann mache dasselbe für den Rechtes-Kind-Zeiger mit dem nächsten Element von \(A\). Danach kommt das nächste Knotenobjekt aus der Queue dran usw. Durch das Verwenden der Queue und durch das Bevorzugen von linken Kindern vor rechten Kindern wird der Baum genau in der richtigen Reihenfolge aufgebaut. In unserem Beispiel passiert folgendes:

Die Operationen der Queue sind jeweils konstant und wir können leicht mit einem Zeiger durch das Array laufen, um die entsprechenden Schlüsselwerte auszulesen.
Nun analysieren wir, was in der for-Schleife passiert. Wir wollen eine obere Schranke zeigen und nehmen deshalb an, dass wir für maximal viele Knoten MinVersickere aufrufen und jeder Aufruf so teuer wie möglich ist. Wir haben uns bereits überlegt, dass die Kosten von MinVersickere für einen Knoten mit Höhe \(k\) in \(\Theta(k)\) liegen, das heißt, die Kosten sind höchstens \(c\cdot k\) für eine Konstante \(c\). Für unsere obere Schranke müssen wir uns somit nur noch überlegen, wie viele Knoten wir versickern und welche Höhe sie jeweils haben, und dann addieren wir alle Kosten einfach auf.
Bei BuildMinHeap beginnen wir im vorletzten Level des Binärbaums und im schlimmsten Fall sind dort alle Knoten auch Väter und jeder Vater hat genau zwei Kinder. Wir nehmen also an, dass auch das letzte Level vollständig gefüllt ist. Mit Hilfe von Lemma 1 gilt deshalb \(n = \sum_{i=0}^h 2^i = 2^{h+1}-1\), wobei \(h\) die Höhe der Wurzel ist. Außerdem gilt, dass das vorletzte Level genau \(2^{h-1}\) Knoten enthält, das vorvorletzte \(2^{h-2}\) usw. bis zum \(0\)-ten Level, das nur die Wurzel und somit \(2^0\) Knoten enthält.
Die Knoten im \(0\)-ten Level, d. h. nur die Wurzel, haben Höhe \(h\) und somit kostet das Versickern der Wurzel höchstens \(c\cdot h\). Die Knoten im ersten Level haben Höhe \(h-1\) und somit kostet das Versickern pro Knoten in diesem Level höchstens \(c \cdot (h-1)\). Allgemein gilt, dass Knoten im Level \(i\), für \(0\leq i \leq h-1\), eine Höhe von genau \(h-i\) haben und somit das Versickern pro Knoten in Level \(i\) höchstens \(c \cdot (h-i)\) kostet.
Wir haben uns bereits überlegt, dass es höchstens \(\frac{n}{2^{h-i}}\) viele Knoten mit Höhe \(i\) gibt.
Für Anzahl der Knoten mit Höhe \(h\) gilt folgendes: Sei \(n(h)\) die Anzahl der Knoten mit Höhe \(h\). Aus Lemma 1 folgt, dass \[n(h) \leq \frac{n}{2^h}\ .\]
Seien \(C(n)\) die Kosten von BuildMinHeap auf einem Array mit \(n\) Elementen, wobei \(2^{h}-1 < n \leq 2^{h+1}-1\). Dann gilt:
\[C(n) \leq \sum_{i=0}^{h-1} 2^{i} \cdot c \cdot (h-i) = c \cdot \sum_{i=0}^{h-1} 2^{i} \cdot (h-i) \leq c \cdot \sum_{i=0}^{h-1} \frac{n}{2^{h-i}}\cdot (h-i)\]
\[
= cn \cdot \sum_{i=0}^{h-1} \frac{h-i}{2^{h-i}} = cn \cdot \left(\frac{h}{2^h} + \frac{h-1}{2^{h-1}} + … + \frac{h-(h-1)}{2^{h-(h-1)}} \right) = cn \cdot \sum_{i = 1}^{h} \frac{i}{2^i}\ .
\]
Es gilt
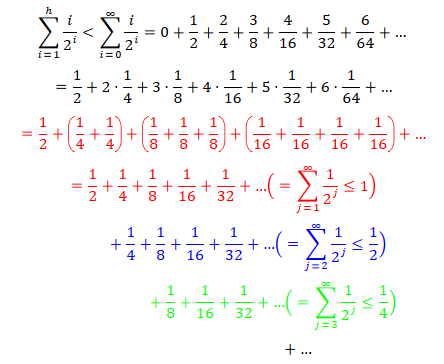
Und damit folgt $\color{black} \sum_{i=1}^h \frac{i}{2^i} < \sum_{i=0}^\infty \frac{i}{2^i} \leq {\color{red}1} + {\color{blue}\frac{1}{2}} + {\color{green}\frac{1}{4}} + … = \sum_{i=0}^\infty \frac{1}{2^i} = 2$. Hierbei haben wir mehrfach die bereits bekannte geometrische Reihe \(\sum_{i=0}^\infty \frac{1}{2^i} = 2\) genutzt.
Damit haben wir bewiesen, dass \(C(n) \leq cn \cdot 2 \in O(n)\) gilt.
\end{proof}
ExtractMin bzw. ExtractMax
Wir wollen folgendes Problem lösen:
\begin{quote}
Gegeben: Ein nichtleerer Min/Max-Heap.
Aufgabe: Gib das Minimum des Min-Heaps bzw. das Maximum des Max-Heaps aus, entferne es aus dem Heap und stelle danach wieder einen korrekten Min/Max-Heap her.
\end{quote}
Die erstbeste Idee wäre, einfach den Schlüssel in der Wurzel auszugeben, ihn zu löschen und dann von unten her mit dem korrekten Schlüsselwert aufzufüllen. Das heißt, bei einem Min-Heap rückt der kleinste Schlüsselwert der Kinder der Wurzel nach oben in die Wurzel und dann werden die Kinder dieses Kindes betrachtet usw, so lange, bis ein leeres Blatt entsteht, das dann einfach gelöscht wird.
Diese Idee führt zwar dazu, dass an allen Knoten die Min-Heap-Eigenschaft gilt, aber es kann passieren, dass der Binärbaum danach nicht mehr die richtige Form hat:

Wir müssen uns daher etwas cleverer anstellen. Die Lösung liegt darin, dass wir dafür sorgen, dass am Ende das richtige Blatt, nämlich das rechteste im letzten Level, gelöscht wird. Das erreichen wir, indem wir die folgenden Schritte ausführen:
ExtractMax funktioniert analog mit MaxVersickere. Wir wissen bereits, dass Min/MaxVersickere für den Wurzelknoten eines Min/Max-Heaps mit \(n\) Knoten Kosten von \(\Theta(\log n)\) verursacht. Das heißt, allein Zeile \(4\) hat schon logarithmische Kosten. Fraglich ist noch, wie in Zeile \(2\) der rechteste Knoten im letzten Level bestimmt wird. Eigentlich haben wir ja nur einen Zeiger auf die Wurzel des Heaps und keinen Direktzugriff auf das rechteste Blatt im letzten Level. Wir werden später sehen, dass man Heaps clever implementieren kann, um dieses Problem zu umgehen.
Allerdings könnte man auch direkt einen Zeiger auf das rechteste Blatt haben (bei Erstellung des Heaps ist das leicht) und ihn dann mit Kosten \(O(\log n)\) aktualisieren, wenn sich das letzte Blatt ändert. Für die Aktualisierung müsste man notfalls bis zur Wurzel und von dort im linken Teilbaum bis zum rechtesten Blatt laufen. (Alternativ wäre es auch möglich, einfach nach dem rechtesten Blatt im letzten Level zu suchen. Dazu müssten wir z. B. noch in jedem Knoten speichern, wie viele Knoten unterhalb dieses Knotens liegen. Damit könnten wir dann von der Wurzel nach unten immer die Anzahlen überprüfen und damit zum richtigen Blatt navigieren. Das würde uns \(O(\log n)\) kosten. Beim Aufbau des Heaps ist das kein Problem. Später, wenn der Heap Knoten verliert, müssten wir das bei den entsprechenden Knoten anpassen. Auch das geht leicht, denn es ändern sich nur die Zählerwerte von Knoten, die auf einem direkten Weg vom gelöschten Knoten zur Wurzel liegen. Insgesamt kostet das \(O(\log n)\).)
Somit gilt, dass ExtractMin in einem Min-Heap bzw. ExtractMax in einem Max-Heap Kosten von \(O(\log n)\) hat.
Heapsort mit Zusatzspeicher
Nun, da wir Heaps kennen, können wir sie nutzen, um zu sortieren. Wir betrachten zunächst die einfachste Variante von Heapsort. Diese Version wird schon eine Worstcase-Laufzeit von \(O(n\log n)\) haben. Allerdings benötigen wir auch noch \(\Theta(n)\) zusätzlichen Speicherplatz. Der Code lautet wie folgt:
Heapsort(\(A\))
Input: Array \(A\) der Länge \(n\)
\begin{algorithmic}
\STATE{\(H \leftarrow\) \textsf{BuildMinHeap(\(A\))}}
\FOR{\(i=0\) to \(n-1\)}
\STATE{\(A[i] \leftarrow\) \textsf{ExtractMin(\(H\))}}
\ENDFOR
\end{algorithmic}

Die Analyse ist nun sehr einfach. Zeile \(1\) kostet uns \(O(n)\). Jeder der \(n\) vielen Durchläufe der for-Schleife kostet höchstens \(O(\log n)\). Somit haben wir insgesamt Kosten in \(O(n\log n)\) im Worstcase. Neben dem Array \(A\) wird allerdings noch \(\Theta(n)\) Speicherplatz für den Min-Heap benötigt. Das heißt, diese Version von Heapsort benötigt recht viel zusätzlichen Speicherplatz.
Array-Implementierung von Heaps
Wir werden nun sehen, dass wir eigentlich gar keine Knotenobjekte brauchen, um einen Heap zu implementieren. Die spezielle Struktur eines Heaps erlaubt es uns, ihn einfach mithilfe eines Arrays zu realisieren. Wir werden das später verwenden, um Heapsort so abzuändern, dass wir nur noch konstant viel Zusatzspeicher benötigen und trotzdem Worstcase-Kosten von \(O(n\log n)\) haben.
Die entscheidende Einsicht liefert uns eine spezielle Nummerierung der Knoten eines gerichteten Binärbaums, der bis auf das letzte Level vollständig ist und bei dem das letzte Level von links her gefüllt ist. Diese Nummerierung haben wir weiter oben sogar schon benutzt.
Wenn wir die Knoten eines solchen Binärbaums von Level \(0\) bis zum letzten Level jeweils von links nach rechts durchnummerieren und diese Zählung bei \(0\) beginnen, dann erhalten wir folgende Eigenschaften:
- Das linke Kind von Knoten \(i\) hat die Nummer \(2i+1\) und das rechte Kind von Knoten \(i\) hat die Nummer \(2i+2\),
- Die Wurzel hat die Nummer \(0\),
- Das rechteste Blatt im letzten Level hat die Nummer \(n-1\).

Somit können wir auch einfach ein Array mit \(n\) Elementen als einen gerichteten Binärbaum mit \(n\) Knoten auffassen, der bis zum vorletzten Level vollständig ist und dessen letztes Level von links her gefüllt ist. (Das ist der eigentliche Grund, warum das letzte Level eines Heaps von links her gefüllt sein muss.) Das Element an Index \(0\) ist die Wurzel, das linke Kind davon steht an Index \(2\cdot 0 +1 = 1\), das rechte Kind steht an Index \(2\cdot 0 + 2 = 2\) usw. Wir benötigen also den Binärbaum überhaupt nicht!
Nun müssen wir nur noch unsere Version von Min/MaxVersickere auf die Array-Implementierung anpassen:
ArrayMinVersickere(\(A,i,j\))
Input: Array \(A\), Indizes \(i\) und \(j\)
\begin{algorithmic}
\IF{\(2i+1>j\)}
\RETURN
\ENDIF
\STATE{\(k \leftarrow 2i+1\)}
\IF{\(2i+2 \leq j\)}
\IF{\(A[2i+1]>A[2i+2]\)}
\STATE{\(k \leftarrow 2i+2\)}
\ENDIF
\ENDIF
\IF{\(A[k]<A[i]\)}
\STATE{vertausche \(A[i]\) mit \(A[k]\)}
\STATE{\textsf{ArrayMinVersickere(\(A,k,j\))}}
\ENDIF
\end{algorithmic}

Für ArrayMaxVersickere müssen lediglich die Ungleichungen in Zeile \(6\) und \(9\) umgedreht werden. Man beachte, dass wir neben dem Index \(i\), der das zu versickernde Element bezeichnet, auch noch einen Index \(j\) mitgeben. Dieser Index markiert den letzten Eintrag im Array, d. h. den rechtesten Knoten im letzten Level des zugehörigen Heaps. Eigentlich ist das unnötig, wenn wir wissen, wie viele Elemente das Array hat. Doch mit diesem Trick müssen wir das nicht jedes Mal abfragen.
Nun kommen wir noch zur neuen Version von BuildMinHeap(\(A\)):
ArrayBuildMinHeap(\(A\))
Input: Array \(A\) der Länge \(n\)\\
Output: \(A\) als korrekter Min-Heap
\begin{algorithmic}
\FOR{\(i = \lfloor\frac{n}{2}\rfloor-1\) downto \(0\)}
\STATE{\textsf{ArrayMinVersickere}(\(A,i,n-1\))}
\ENDFOR
\RETURN \(A\)
\end{algorithmic}

Man beachte, dass an Index \(\lfloor\frac{n}{2}\rfloor -1\) der rechteste Vater im vorletzten Level steht. Es genügt, bei ihm zu beginnen und sich dann Level für Level nach oben, jeweils von rechts nach links, zu arbeiten. Genau diese Reihenfolge erhalten wir auch, wenn wir die Nummerierung umgekehrt ablaufen.
Heapsort ohne Zusatzspeicher
Wir haben eben gesehen, dass wir das Eingabearray auch direkt als Heap auffassen können. Damit gelingt es uns, Heapsort mit nur konstant viel Zusatzspeicher zu realisieren. Allerdings benötigen wir dazu noch einen Trick: Wir werden statt eines Min-Heaps einen Max-Heap verwenden! Außerdem benötigen wir ExtractMin/Max überhaupt nicht. Uns genügt ArrayBuildMaxHeap und ArrayMaxVersickere.
Wir benutzen einen Max-Heap, da wir ja eigentlich nach und nach Elemente aus dem Heap entfernen wollen. Im Array bedeutet das, dass wir uns die hintersten Elemente nicht mehr anschauen, da sie dann nicht mehr zum Heap gehören. Wenn wir aber aufsteigend sortieren wollen, dann müssen in den hinteren Zellen des Arrays aber die größten Werte stehen! Und genau die liefert uns ein Max-Heap.
ArrayHeapsort(\(A\))
Input: Array \(A\) mit Länge \(n\)
\begin{algorithmic}
\STATE{\textsf{ArrayBuildMaxHeap(\(A\))}}
\FOR{\(i=n-1\) downto \(1\)}
\STATE{vertausche \(A[0]\) mit \(A[i]\)}
\STATE{\textsf{ArrayMaxVersickere(\(A,0,i-1\))}}
\ENDFOR
\end{algorithmic}

Zu beachten ist, dass in Zeile \(4\) von ArrayHeapsort jeweils in einem Max-Heap versickert wird, der einen Knoten weniger, nämlich den jeweils rechtesten Knoten im letzten Level, enthält. Das ist genau der Index, zu dem wir das aktuelle Maximum getauscht haben. Damit wird verhindert, dass das so eben getauschte Maximum wieder nach oben rückt.
Heaps als Priority-Queue
Min/Max-Heaps werden häufig als Implementierung einer Priority-Queue genutzt. Eine Priority-Queue ist jede Datenstruktur, die die Operationen Insert (ein neues Element mit einem Prioritätswert einfügen), ExtractMin (das Element mit der kleinsten/größten Priorität entfernen und ausgeben) und DecreaseKey (den Prioritätswert eines Elements verringern/erhöhen) unterstützt.
Wir haben bereits ExtractMin behandelt. Es fehlen noch Insert und DecreaseKey.
Insert:
Insert in einen Min/Max-Heap mit \(n\) Knoten geht ganz leicht mit Kosten \(\Theta(\log n)\), wenn wir den Min/Max-Heap nicht als Array, sondern als gerichteten Binärbaum speichern. (Natürlich können wir auch einfach ein dynamisches Array verwenden. Das ist deutlich speichereffizienter.) Dabei nehmen wir an, dass wir einen Zeiger auf den linkesten Vater \(p\) haben, der nicht zwei Kinder hat. (Diesen Zeiger kann man leicht nach jedem Einfügen wieder aktualisieren. Übrigens müssen wir bei \(p\) einfügen, da wir sonst die Strukturvorgabe des Min/Max-Heaps verletzen.) Insert funktioniert, wie folgt:
- Füge den neuen Schlüssel als linkes Kind von \(p\) hinzu, falls \(p\) keine Kinder hat, sonst als rechtes Kind von \(p\).
- Beginne beim neueingefügten Schlüssel und versickere nach oben. Das heißt, tausche so lange den Schlüssel mit dem Schlüssel des Vaterknotens, bis die Min/Max-Heap-Eigenschaft wieder hergestellt ist.
Hier ein Beispiel:

DecreaseKey:
DecreaseKey können wir auch leicht in \(\Theta(\log n)\) ausführen, sofern wir einen Zeiger direkt auf den entsprechenden Knoten (bzw. den Index bei Arrayimplementierung) im Min/Max-Heap haben. Diese Zeiger zu verwalten ist leicht. Wir können sie einfach als weiteres Attribut an jedes Knotenobjekt im Graphen schreiben. Mithilfe dieses Zeigers können wir somit direkt auf den zu ändernden Schlüssel im Min/Max-Heap zugreifen. Nach Änderung müssen wir dann wie bei Insert evtl. noch nach oben versickern.
Zusammenfassung
Heapsort sortiert, indem ein Heap genutzt wird, um iterativ jeweils das größte bzw. kleinste Element zu ermitteln. Ein solcher Min/Max-Heap kann in Linearzeit aufgebaut werden. Und falls wir irgendwo eine Schlüsseländerung haben, z. B. durch einen Tausch, dann kann in logarithmischer Zeit die Min/Max-Heap-Eigenschaft wieder hergestellt werden.
Wenn wir Heaps clever implementieren, dann können wir sie direkt im Eingabearray speichern und somit auf zusätzlichen Speicher verzichten. Die Laufzeit von Heapsort ist für jede Eingabe (mit unterschiedlichen Schlüsselwerten) in \(O(n\log n)\), da immer in \(\Theta(n)\) ein Heap aufgebaut wird und dann jeweils \(n\)-mal versickert wird. Versickern kostet höchstens \(O(\log n)\).
Wenn wir Heaps als Priority-Queue nutzen, dann können wir damit leicht die Operationen Insert, ExtractMin und DecreaseKey jeweils in \(O(\log n)\) realisieren.

